3 Vignette 3: Landslides
Adam Booth
Theory
Experimental data from a wide range of earth surface materials, including most soils and rocks, show that they are Mohr-Coulomb materials, where their shear strength is determined as follows:
Mohr-Coulomb materials
| [latex]τ_s=c+σ′tan(φ)[/latex] | (1) |
where
- [latex]τ_s[/latex] is the shear strength [M L-1 T-2]
- [latex]c[/latex] is cohesion [M L-1 T-2]
- [latex]σ′[/latex] is the effective normal stress [M L-1 T-2]
- and [latex]φ[/latex] is the angle of internal friction [degrees]
Effective normal stress
Shear strength therefore depends linearly on effective normal stress, such that cohesion is the intercept and [latex]tan(φ)[/latex] is the slope of the relationship. In other words, cohesion is the amount of strength present in the absence of any effective normal stress, while [latex]tan(φ)[/latex] determines how much additional shear strength the sample gains as effective normal stress increases. To determine these two parameters, samples of material are deformed at different effective normal stresses in a laboratory, and a line is fit to the data.
In eq. (1), the strength depends on the effective normal stress, rather than the total normal stress. Effective normal stress is defined as normal stress minus the pore fluid (water) pressure:
Effective normal stress
| [latex]σ′=σ-p[/latex] | (2) |
where
- [latex]σ[/latex] is normal stress [M L-1 T-2]
- and [latex]p[/latex] is pore pressure [M L-1 T-2]
For completely dry conditions, the effective normal stress is therefore equal to the normal stress. However, when the material is saturated with water, pore pressure becomes positive, and therefore reduces the effective normal stress. This reduces the material’s strength. In standard slope stability analysis, this is the only role that water plays. Water does not affect the cohesion or friction angle, only the effective normal stress.
Factor of safety
Now that a soil’s or rock’s shear strength is defined, it must be compared to the shear stress acting on it to determine whether or not it will fail. Engineers and geologists commonly use the factor of safety to make this comparison:
Factor of safety
| [latex]F=τ_s/τ[/latex] | (3) |
where
- [latex]F[/latex] is the factor of safety [unitless]
- [latex]τ_s[/latex] is the available shear strength [M L-1 T-2]
- and [latex]τ[/latex] is the driving shear stress [M L-1 T-2]
So the factor of safety is the ratio of strength available to resist failure to the stress driving failure. If available strength is greater than stress, [latex]F>1[/latex], and the slope is stable. In this stable scenario, note that even though more strength is available, only a portion of that strength is actually acting to resist the shear stress. Otherwise the stresses would be unbalanced, and the landslide would be accelerating uphill, the direction in which the strength acts.
Mobilized shear strength
The amount of strength required to exactly balance the stress is called the mobilized shear strength. If available strength is equal to stress, [latex]F=1[/latex], and the slope is at the threshold of instability. If available strength drops below stress, [latex]F<1[/latex], and the slope should be actively failing, i.e. accelerating in the downslope direction.
Eq. (3) is a general statement, but determining the shear and normal stresses requires a set of assumptions for the potential landslide’s geometry. The most common approach, which is also the starting point for more complicated and realistic approaches, is to assume an infinite slope.
More specifically, the infinite slope approach assumes a hillslope has a uniform inclination and extends to infinity in all directions, and there is a potential failure plane for the landslide at a constant depth below the surface, such that its inclination is the same (Fig. 1). Subsurface water is also assumed to be slope-parallel seepage, so that pore water pressure can be determined by the height of the water table above the failure plane.
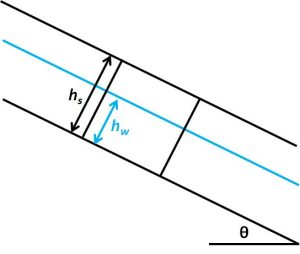
With these assumptions, one can consider a column of potential landslide material above the assumed failure plane, ignore stresses on the top and sides of the column, and resolve shear and normal stresses on the column’s base. First, the weight of the column, [latex]W[/latex] [M L T-2], is given by
| [latex]W=ρ_sgh_sΔxΔy[/latex], | (4) |
where [latex]ρ_s[/latex] is the landslide material (e.g. soil) density [M L-3], [latex]g[/latex] is acceleration due to gravity [L T-2], [latex]h_s[/latex] is the slope-normal height of the column of landslide material above the failure plane [L], and [latex]Δx[/latex] and [latex]Δy[/latex] are the slope-parallel dimensions of the column base [L].
Since the failure plane is inclined with respect to horizontal, the column’s weight can be resolved into its slope-normal, [latex]W_n[/latex], and slope-parallel, [latex]W_p[/latex], components:
| [latex]W_n=ρ_sgh_sΔxΔycos(θ)[/latex], | (5) |
| and [latex]W_p=ρ_sgh_sΔxΔysin(θ)[/latex], | (6) |
where [latex]θ[/latex] is the angle of the failure plane from horizontal [degrees]. To convert these forces to stresses, divide them by the area of the column base, [latex]ΔxΔy[/latex], which results in
| [latex]σ=ρ_sgh_scos(θ)[/latex], | (7) |
| and [latex]τ=ρ_sgh_ssin(θ)[/latex]. | (8) |
Last, to get the effective normal stress, which is needed to determine shear strength, note that the pore water pressure is the weight of the water divided by the area of the column base:
| [latex]p=ρ_wgh_wcos(θ)[/latex], | (9) |
where [latex]ρ_w[/latex] is the density of water, and [latex]h_w[/latex] is the slope-normal height of the water table above the failure plane. Substituting eqs. (7)-(9) into eqs. (1)-(3) leads to the factor of safety equation for an infinite slope with slope-parallel seepage:
Infinite slope stability with slope-parallel seepage
| [latex]F=\frac{c+(ρ_sh_s-ρ_wh_w)gcos(θ)tan(φ)}{ρ_sghsin(θ)}[/latex] | (10) |
Alternatively, it may be more convenient to use the degree of saturation,
| [latex]m=h_w/h_s[/latex], | (11) |
where [latex]m[/latex] [unitless] varies between 0 and 1 depending on the relative height of the water table above the failure plane. This leads to an equivalent form of the infinite slope stability equation:
Infinite slope stability with slope-parallel seepage (alternate form)
| [latex]F=\frac{c+(ρ_s-mρ_w)h_sgcos(θ)tan(φ)}{ρ_sghsin(θ)}[/latex] | (12) |
Eqs. (10) and (12) can be used directly to calculate the factor of safety of a slope with known or assumed material properties ([latex]ρ_s[/latex], [latex]c[/latex], and [latex]φ[/latex]), geometry ([latex]θ[/latex], [latex]h_s[/latex]), subsurface hydrologic conditions ([latex]h_w[/latex]), and even planetary setting ([latex]g[/latex]).
Alternatively, one can calculate conditions under which a slope would likely fail by setting [latex]F=1[/latex] and then solving for the parameter(s) of interest. Similarly, [latex]F=1[/latex] is assumed for back analysis of a landslide that already occurred to determine its strength properties and/or hydrologic conditions at the time of failure.
case study: Southeast Alaska
For this case study, first read this vignette summarizing the effects of forest changes on landslides in southeast Alaska. Two main ways that forests promote slope stability are through the strength of their root systems, which effectively increases cohesion, and through interception and evapotranspiration, which reduce subsurface pore water pressures.
The following example illustrates the large effect than changes to root cohesion can have on a hillslope’s factor of safety. When a tree dies, but its roots remain in the ground, the strength of those roots typically decays exponentially over the following years to decades, and the underlying slope is more vulnerable to failure.
Example: Calculating factor of safety for varying cohesion
Assume a hillslope in southeast Alaska has the following properties:
- Slope angle of 36º (the mean slope where landslides occurred in the Vignette).
- Failure plane depth of 0.7 m (a relatively large soil depth for the site).
- Degree of saturation of 50% (which occurs with 54 mm of precipitation at the site).
- Soil density of 1600 kg/m3.
- Soil friction angle of 33º.
First, assume that the hillslope is forested with healthy trees, and the effective cohesion including roots is 50 kPa. To calculate the hillslope’s factor of safety, plug all the relevant values into eq. (12):
[latex]F=\frac{(50,000Pa)+((1,600kg/m^3)-(0.5)(1,000kg/m^3))(0.7 m)(9.8m/s^2)cos(36^{\circ})tan(33^{\circ})}{(1,600kg/m^3)(9.8m/s^2)(0.7m)sin(36^{\circ})}[/latex].
Calculating all the products then gives
[latex]F=\frac{50,000Pa+3,965Pa}{6,452Pa}[/latex],
so most of the hillslope’s strength comes from root cohesion. The factor of safety with healthy trees is then [latex]F=8.4[/latex], and the slope is predicted to be stable. There is more than eight times as much strength available than is needed to balance the driving shear stress.
Now assume, some of the trees have died, and root cohesion has dropped to 5 kPa in the subsequent years. To determine the effect of this change in root strength alone, plug in the new cohesion value, while leaving everything else the same:
[latex]F=\frac{5,000Pa+3,965Pa}{6,452Pa}=1.4[/latex].
The factor of safety has dropped considerably, and now the strength provided by roots is the same order of magnitude as the strength provided by friction. There is about 40% more strength available than is needed to balance the driving stress.
Last, assume the trees have been dead for many years, and their roots no longer provide any cohesive strength. Substituting [latex]c=0[/latex] kPa gives a factor of safety of
[latex]F=\frac{0Pa+3,965Pa}{6,452Pa}=0.6[/latex].
Since [latex]F<1[/latex], the slope should now be unstable. In southeast Alaska, according to the vignette, this would likely happen during a rainstorm that produces just a few centimeters of precipitation, a common occurrence in the area.
